引言:
ACEE信息理论课程笔记, 好难的数学。(信息的度量,信息的无损压缩,信息的传输1-3章)
信息的度量
随机变量的熵和互信息
概率论的一些基本概念
- 我们定义随机变量的概率空间
的取值空间, 事件 发生的概率,
联合变量对:
二维随机变量
对于二维随机变量
的边际概率分布: 的边际概率分布:
对于条件概率,有:
事件的自信息
- 事件的信息量基于该事件发生的概率
- 定义:对于概率空间
事件 的自信息定义为:
单位:当a=2时,为比特(bit),当a=e时,为奈特
特点:
- 事件发生的概率越小,事件的信息量越大
- 两事件的信息量之和,信息量相加,概率相乘
事件的条件自信息,事件
发生的条件下事件 的条件自信息定义为:
事件的互信息
- 事件
与事件 之间的互信息定义为;
事件互信息的本质:一个事件对另一个事件不确定性的降低
事件互信息的对称性:
事件的联合自信息的定义
- 事件
和 的联合自信息定义为:
- 表示两事件同时发生需要的信息量,或者同时发生后对外界提供的信息量
事件的条件互信息
- 在给定
的条件下,时间 与 之间的条件互信息为:
事件的联合互信息
- 联合事件
与事件 之间的互信息:
- 表示事件
联合提供给事件 的信息量
需要注意:
- 时间的自信息,条件自信息都大于0,而事件的互信息可小于,大于,等于0
随机变量的熵
- 定义:随机变量的熵定义为随机变量各个事件的平均自信息
- 熵与自信息的区别:熵针对的是随机变量,自信息针对具体事件
随机变量的联合熵
表示两个随机变量的不确定性度量
随机变量的条件熵
- 定义:给定
的条件下,X的条件熵为:
- 定义:随机变量
相对于随机变量 的条件熵为
- 性质:当X和Y统计独立时,
随机变量联合熵的链式法则
- 随机变量X和Y的联合熵的链式法则:
- 性质:当X和Y统计独立时,
,
熵的性质
- 有如下性质:
对概率矢量 的分量是对称的 - 非负性,即
- 确定性,即若
中有一个分量为1,其余均为0,则 - 可扩展性,即
熵的可加性
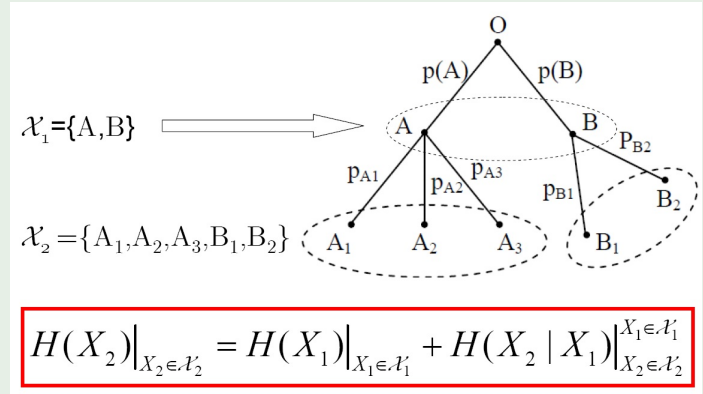
如图,在这种情况下,有如下等式:
对变量X可以进行多步分层的观察,每一步都可从上一步的观察结果中得到更为细致的结果,变量X在最后的观察结果集合中的不确定性等于第一次观察结果的不确定性,加上其后每次观察结果在前一次观察结果已知的前提下的条件不确定性。
熵的极值性
- 性质:条件熵
熵:增加条件使熵减少
熵的凸性
是 的严格上凸函数,即对任何 , 和任何二个 维概率矢量 有:
凸函数的性质:
不等式:
随机变量的加权熵*
随机变量的Renyi熵*
随机变量间的平均互信息
两个事件
互信息的性质
- 非负性:
- 对称性:
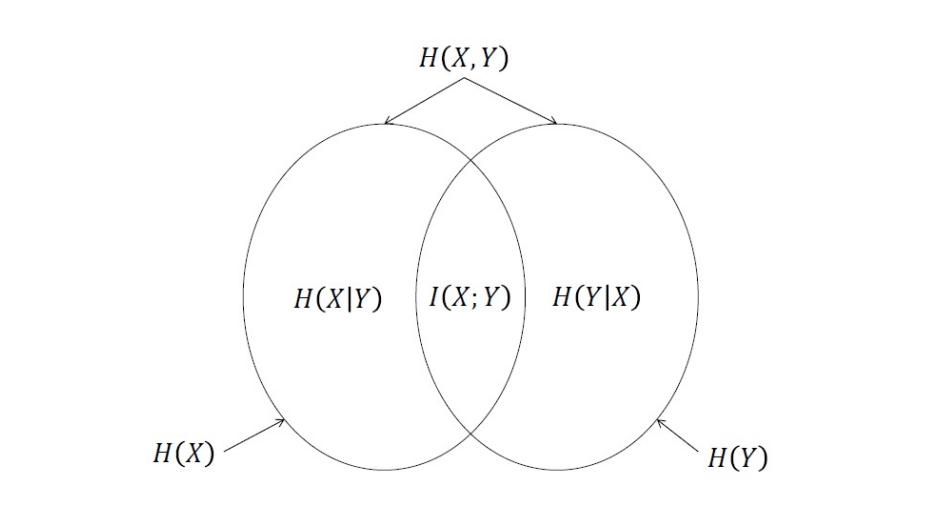
由此可得:
条件互信息
事件的条件互信息:
联合互信息
事件的联合互信息:
相对熵(散度)
定义在相同字符表
性质:
- 若P1,P2是独立分布,并且联合分布是
,如果 是独立分布,并且联合分布是 ,则
关于疑义度的Fano不等式
定义在相同字符表
马尔科夫链

- 定义:如果随机变量序列
的联合概率分布可以写成如下形式:
则称这
- 如果
那么:(越近越大)
- 如果
则:
互信息的凸性
互信息有凸性。。。。(PPT看不明白一点)
连续随机变量的互信息和微分熵
连续随机变量的概率密度
是连续随机变量 的联合概率密度函数 是 的边际密度函数 是Y的边际概率密度
有
连续随机变量的离散化

联合概率分布:
连续随机变量的互信息
联合连续随机变量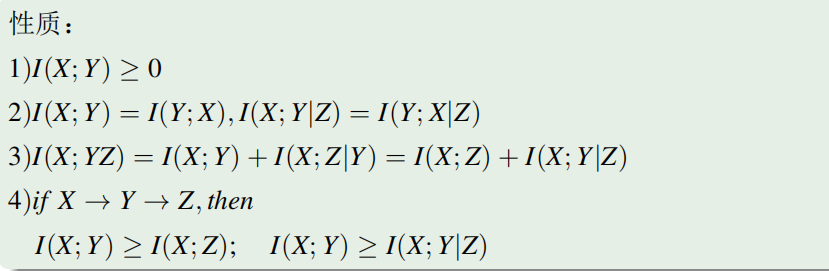
连续随机变量的微分熵
连续随机变量
定义连续随机变量
微分熵的本质和性质
性质:
- 微分熵
不反映连续随机变量 的不确定性,连续随机变量的不确定性一般都是无穷大。但微分熵在一定程度上反映了该连续随机变量的相对不确定性。 可正可负可为0
条件微分熵和联合微分熵及其性质
$$ H_C(X,Y)=-p_{XY}(x,y)log,p_{XY}(x,y)dxdy \ H_C(X|Y)=-p_{XY}(x,y)log, p_{X|Y}(x|y)dxdy \ H_C(X,Y)=H_C(X) + H_C(Y|X) = H_C(Y)+H_C(X|Y) \
H_C(U^N)=H_C(U_1,U_2,,U_N)\={n=1}^NH_C(U_n|U_1,U_2U{n-1})\=_{n=1}^N H_C(U_n|U^{n-1})
\
- 微分熵在线性变化下不具有不变性
即,对于离散随机变量
对于连续随机变量
微分熵的极大化:峰值受限
定理:设X取值限于
等号在均匀分布时达到。
微分熵的极大化:平均功率受限
定理:在方差
即:
熵功率
熵功率的定义:
有如下熵功率不等式:
平稳离散信源的熵
平稳随机过程
定义:对于任意的
平稳随机过程的性质:
平稳离散信源的定义
- 平稳信源:任意长度片段的联合概率分布与时间起点无关:
- 简单无记忆信源:不同时间的随机变量不想管
当m=1时,称为马尔科夫信源
平稳信源的熵
如果一个平稳信源发出长度为N的序列
平均每符号熵:
熵速率:
平均条件熵:
性质:
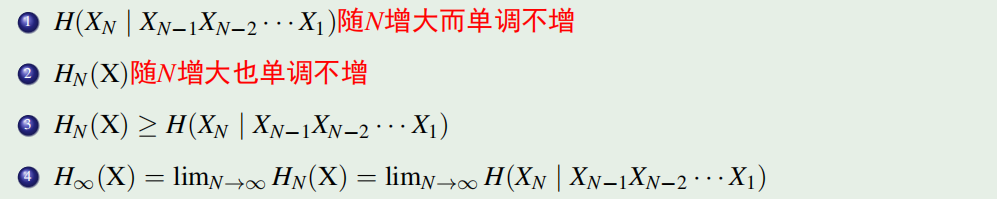
- 熵的相对率:
- 信源的冗余度:
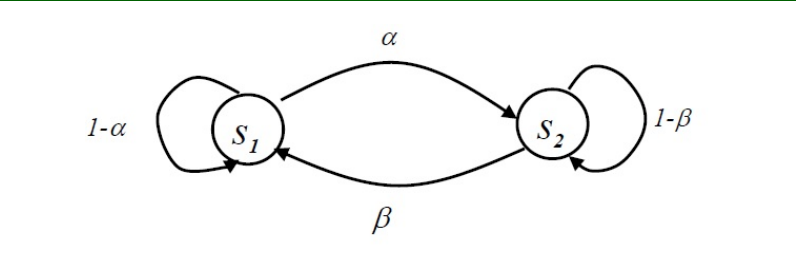
马尔科夫信源
- m阶马尔科夫信源:
- 马尔科夫信源的状态空间:
- 特点:
- 状态空间有限
- 有状态转移函数确定:
时齐既约马尔科夫源的稳态状态分布
时齐:状态转移概率
既约:从任意状态触发,经有限步总可以到达任一其他状态
状态转移矩阵:
n时刻的状态概率分布:
其中:
二元一阶马尔科夫源的熵率:
信息的无损压缩
等长编码
离散无记忆信源(DMS)

离散无记忆信源
字符表
概率分布:
输出长度为
编码
- 编码字符表
- 编码长度:
- 无损编码:
整数编码
- 编码字符表
- 编码字符表
- 则
- 则
可以看出,信源的输出序列越长,编码效率就越高,接近
编码序列越长,译码时延也越长
香农编码定理
- 当
- 当
- 编码速率:
- 无损编码指信源编码的错误概率可以任意小,但并非是0
- 香农编码定理通常是对非常长的消息序列进行编码,特别当消息序列长度
典型列
当长度为
典型列出现的概率为:
典型列几乎等概率
当
对典型列编码, 编码速率为
渐进等分性质
长度为
序列发生的概率:
序列的自信息:
若定义随机变量
由切比雪夫不等式和一堆我看不懂的证明可得:
典型列集及典型列的性质
令
我们给出:
典型列性质
- 当
离散无记忆信源输出序列
不等长编码
DMS的不等长编码
性质:
唯一可译性
- 非奇异:
- 码扩展:
如果码的任意扩展都是非奇异的,则称码是唯一可译的
- 非奇异:
即时可译性
平均码字长度:

为判定一种不等长编码是否满足唯一可译性和即时可译性,我们引入一种判定方法:
即可以判定一种码是否是唯一可译的,即通过其唯一可译性可以确定它是即时可译的。
Sardinas & Petterson 判据
- 核心算法:后缀分解
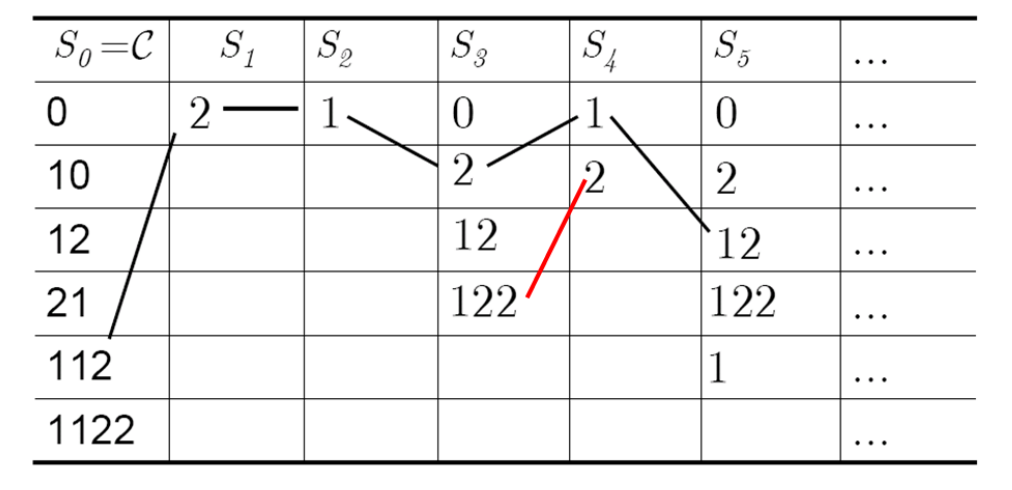
现在我们有码字
- 从
- 之后,从上到下查
- 重复上述操作继续向下迭代直到有以下几种情况:
- 在后续的任意分解集中出现
- 某后缀分解集无法再继续分解——是唯一可译码
- 在后续的任意分解集中出现
由此我们可知:
- 一个码是唯一可译码的充分必要条件是除
即时可译性与唯一可译性的判定
- 若
- 若
异字头码
- 如果一个码中没有任何一个码字是其它码字的前缀,则称该码是异字头码,即
异字头码必为唯一可译码与即时可译码
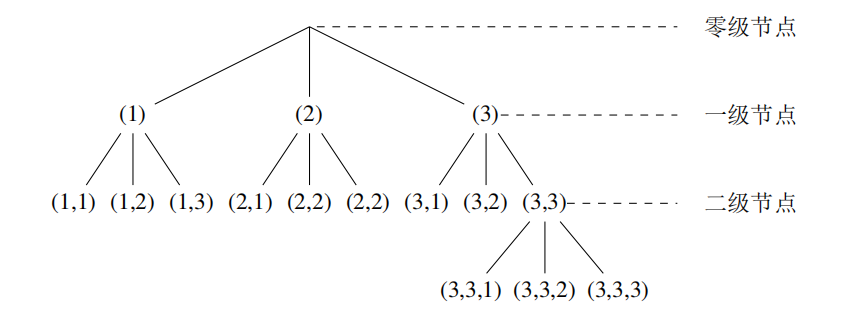
- 在异字头码的树形表示中,可以发现所有的码字都只出现在叶节点上
如果有非叶子节点为码字,则其必为其叶子结点的前缀,不满足异字头码的规定。
Kraft不等式
- 存在长度为
任何唯一可译码必然满足Kraft不等式
唯一可译码与异字头码的关系
- 唯一可译码
- 存在一个同样长度的异字头码
不等长编码定理
- 任意一个唯一可译码得到平均码字长度必须满足
- 证明,,,去tmd吧,证了三页PPT,干啥啊
不等长编码定理的扩展
- 对于长为
即:
- 编码速率:
即:
- 编码效率:
Huffman编码(最佳不等长编码)
- 最佳不等长编码:给定信源分布,在平均码长最短的意义上最佳
- 二元最佳码:给定信源分布,则最佳二元编码必然满足:
- 其出现概率越小的消息所对应的码长越长
- 出现概率最小的两个消息所对应的码长相等,且码字最后一位不同
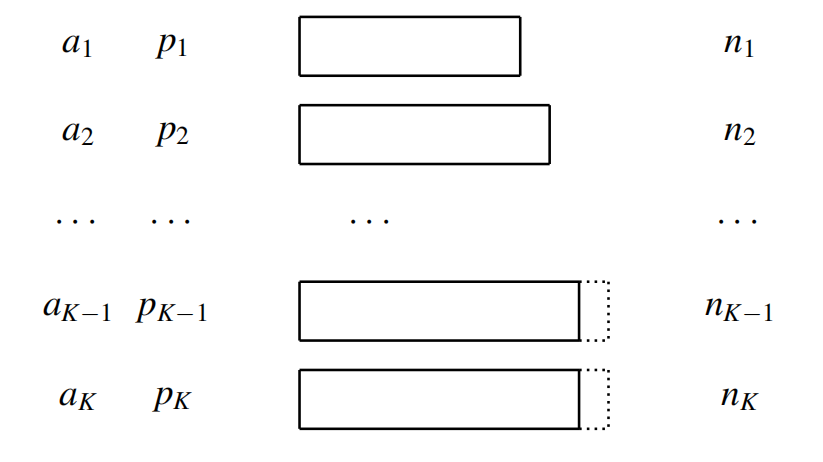
- 首先对各个字符出现的概率从高到低进行排序(从上到下)
- 霍夫曼编码满足以下几条性质:
- 对
霍夫曼编码是一个递归的编码,
可递归编码原理
- 辅助源:设有矩阵
则其辅助源
对辅助源的最佳编码也是对原始源的最佳编码
Huffman编码原理
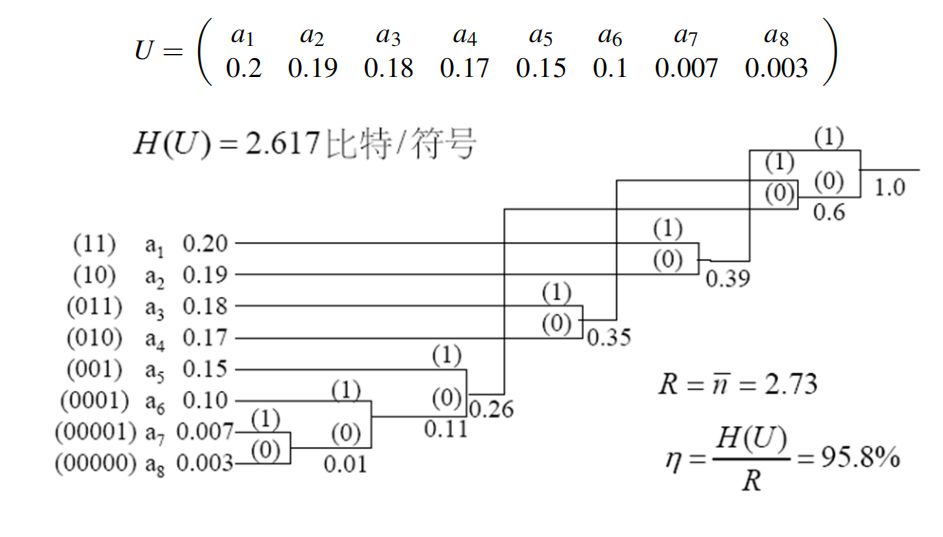
首先我们有一个原始源
从下到上进行消息的合并,概率的相加,即创建原始源的辅助源,原始源中被合并之后的两个消息整体对应辅助源中的一个消息.
即图中
比较
重复(3)过程,直到迭代生成的辅助源中只有一个字符,即
例如
的编码,由根节点,先走 的路径到达子节点,再走 的路径到达 ,则 的编码为
D元Huffman编码
- 若
- 若
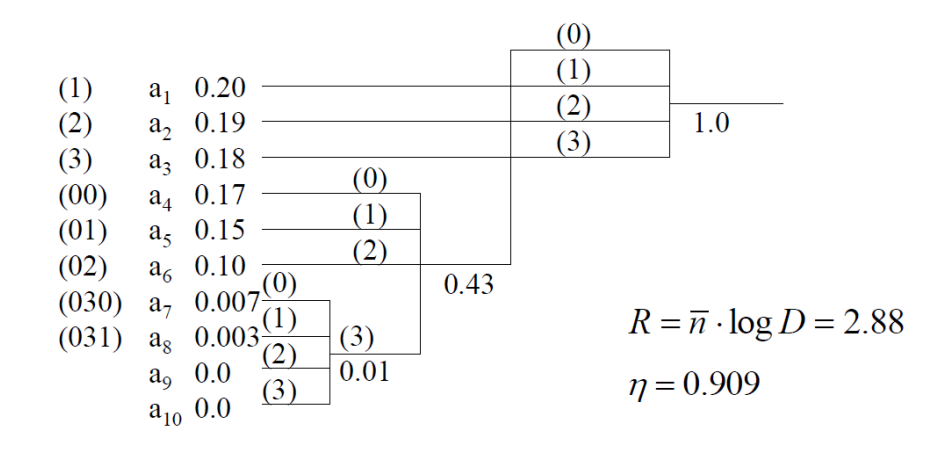
反正用CS一点的话就是,,,二元的霍夫曼编码一个节点有俩孩子,D元每个节点就要有D个孩子,为了保证合并到最后的根节点也必须有
个孩子,就需要去补一些虚拟节点,使得倒数第二次合并的时候仍然有D个节点可以合并(倒数第二次合并的时候节点数可以为D,也可以为D+1)。
- 缺点:每次合并之后都要进行排序,时间复杂度
几种不等长编码
Shannon 编码
原始源:
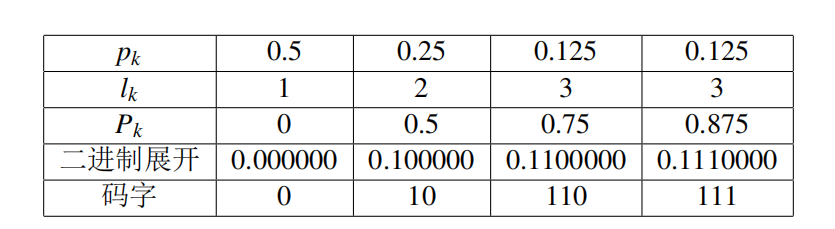
其
如果把长度为
证明
与
Fano编码
- 将原始源切一刀:
- 概率和对分法:
所以实际上
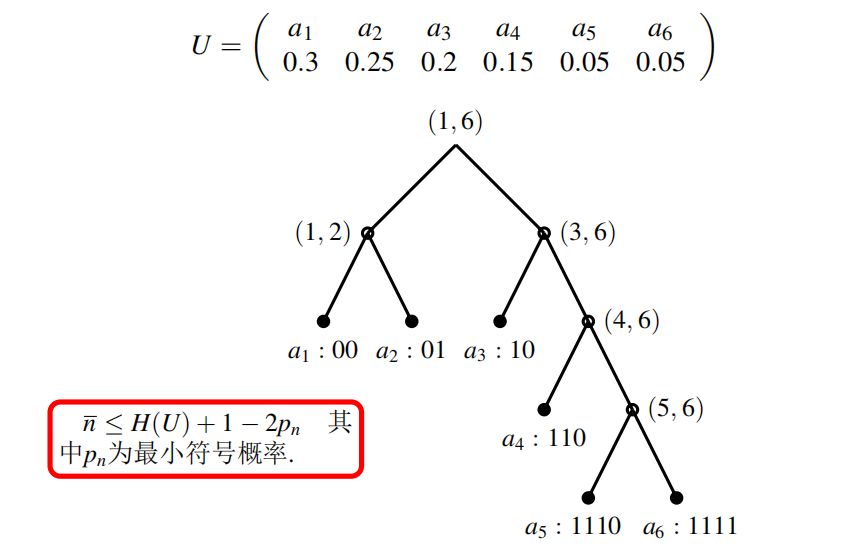
从上到下进行左右子树的延伸,从根节点出现,向左标0,向右标1,生成各个叶子结点的编码。
Shannon-Fano-Elias 编码
信息的传输
离散无记忆信道容量与信道的组合
信道的抽象数学模型
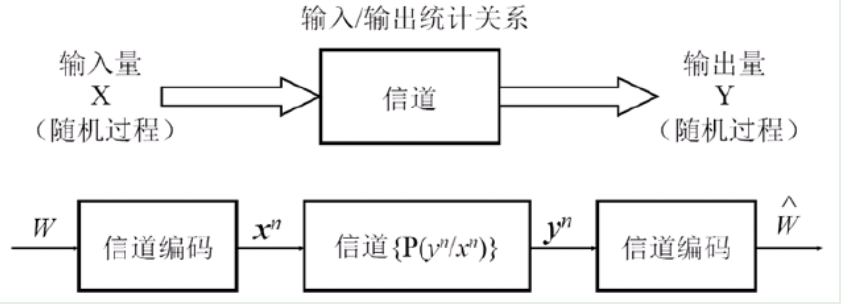
离散无记忆信道
平稳信道
信道容量
信道容量为输出序列对不同输入序列所提供的最大互信息
离散无记忆信道容量
对于离散无记忆信道(DMC)
因此
无噪信道
每个确定的x映射一个确定的y
无损信道
每一个y都可以唯一确定一个x

确定信道
每一个x都可以唯一确定一个y
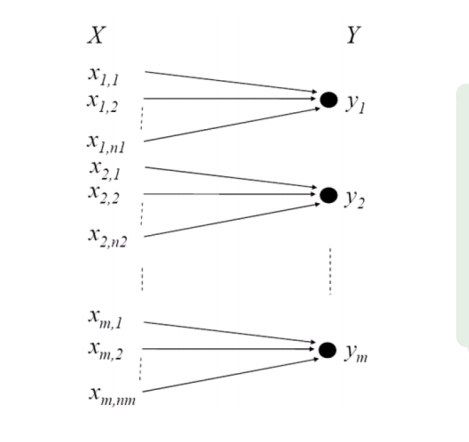
无用信道
不能通过x确定y,也不能通过y确定x
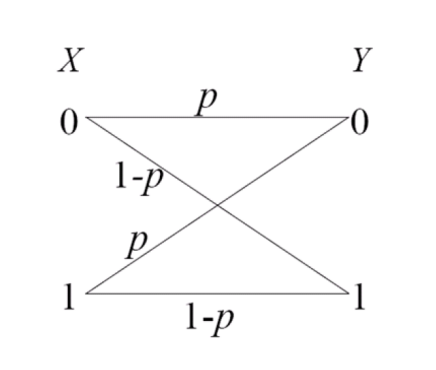
复制信道
每个x可以等同地确定两个y,每个y可以等同确定两个x 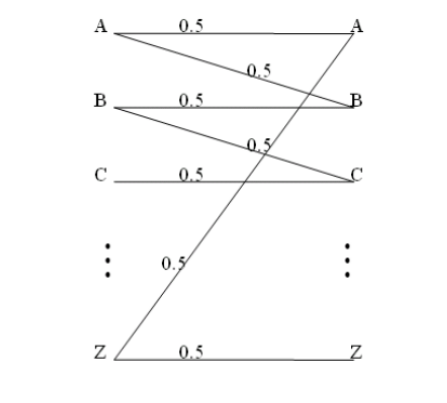
二元对称信道(BSC)
当输入取等概分布时,输出Y也是等概分布。 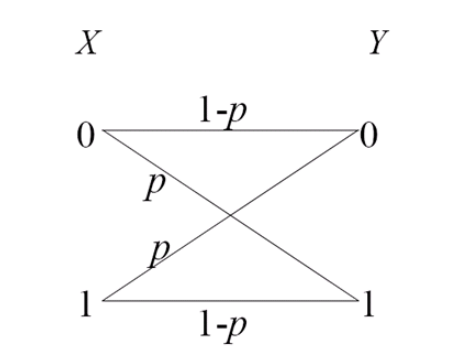
二元除删信道
信道的组合
平行信道
开关信道
级联信道
离散无记忆信道的容量定理
离散无记忆信道的容量定理
- 优化目标
- 约束条件
- 定理:概率分布
其中
凸优化
。。。。
对称离散无记忆信道
离散无记忆信道的转移概率用
我们定义:向量
人话就是,假如一个向量是1,2,3,4。 那只要把这四个数任意打乱顺序,2,3,1,4; 2,4,1,3 ;等等,都叫这个向量的一个置换向量
- 若
- 若
- 若一个信道既关于输出对称,又关于输出对称则该信道是对称的:

准对称离散无记忆信道
对一个信道的转移概率矩阵
例如:
准对称离散无记忆信道的容量定理
- 达到准对称离散无记忆信道容量得到输入分布为均匀分布
- 若信道对于输入对称:
- 若信道同时也关于输出对称:
- 若信道只关于输入对称:
K元对称信道的容量
除删信道的容量
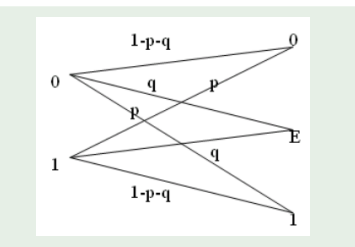
由于准对称信道的输入分布的均匀的:
模K加法信道的容量
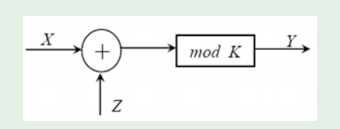
- 模K加法信道:
该信道是一个对称信道
当
转移概率矩阵可逆信道容量
要求
假设
中间证明过程如下,看不懂了
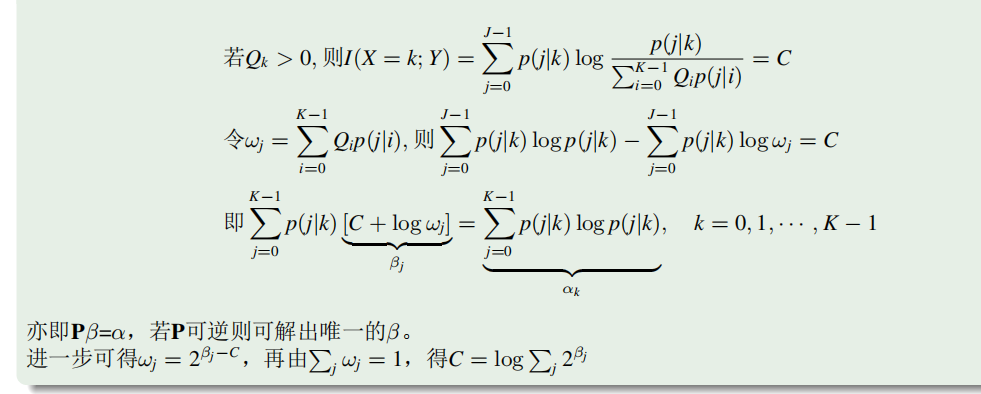
最后就是得到了:
可以求出:
例题:
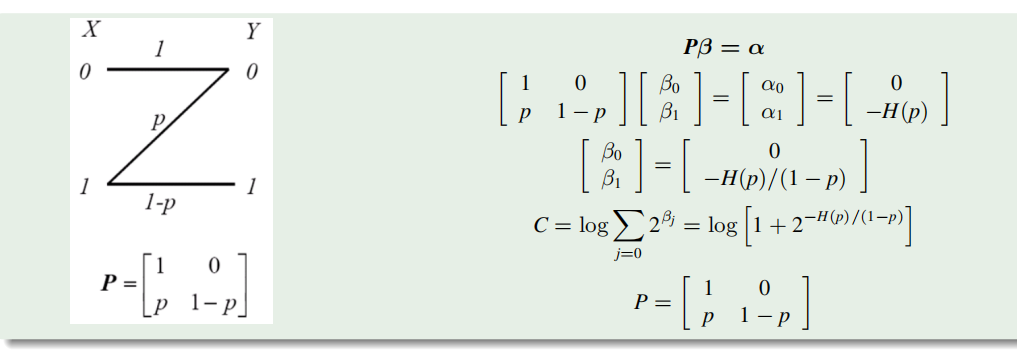
离散无记忆信道的编码定理
离散无记忆信道的编码定理
使用一种编码方法控制

编码速率(传输率):
香农信道编码定理:
如果信息传输速率R小于信道容量C,则总存在一种编码方法,使该信息在该信道上无错误的可靠传输
所有低于信道容量
逆定理:具有
假如
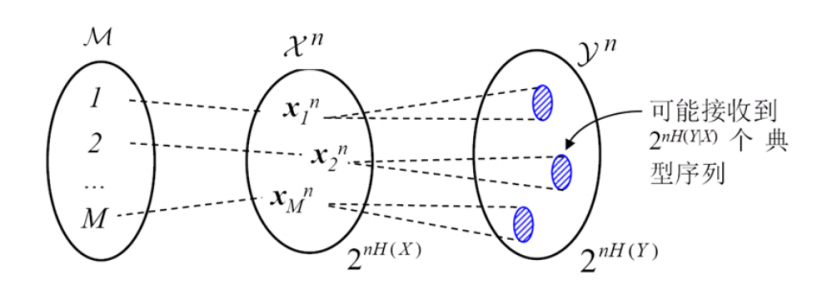
且
离散无记忆信道
- 与
- 编码器,把消息
- 一个码的全体码字构成码书
- 译码器
- 与
发送第
- 最大错误概率定义为
- 平均错误概率
- 若存在一系列
- 最大错误概率定义为
如果
码的平均错误概率 , 则至少有一半的,码字的最大错误概率小于
- 考虑极限情况,一半的码字错误概率
, 一半码字错误概率为 意味着
码的最大错误概率 , 即码率 是可达的
二元对称信道的编码定理
- 码书矩阵:

- 译码方法:如果接收到的
- 译码错误:
联合典型列
相对于联合分布

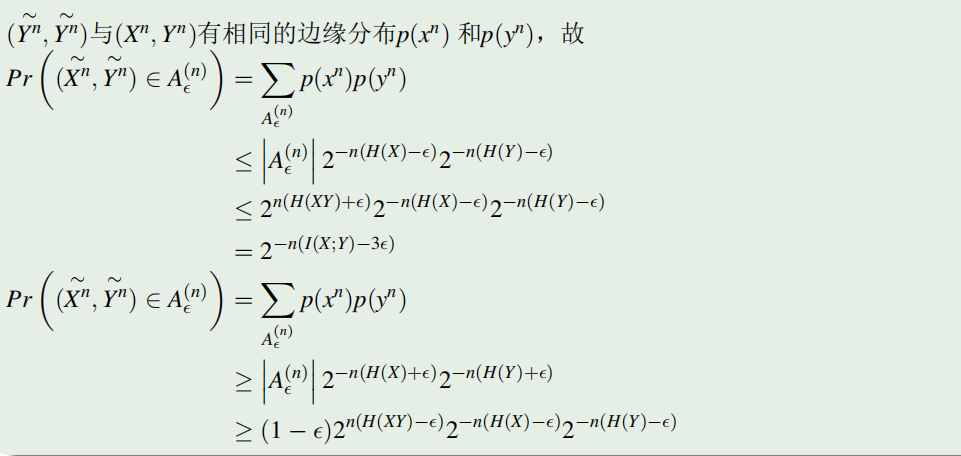
随机选择
加性高斯噪声(AWGN)信道
时间离散的加性高斯信道
给定信道: 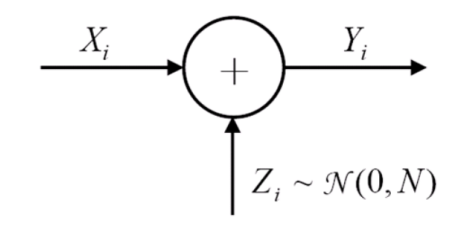
其中
幅度离散化
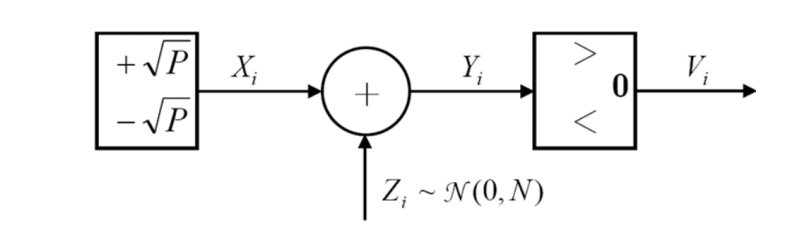
由此可知:
将其变为二元对称信道
加性高斯信道的容量
容量为其最大的互信息:
由于X和Z独立,所以:
加性高斯信道的容量的意义
- 发送信号采用高斯分布时,互信息最大
- 干扰信道(噪声信号)为高斯分布时,互信息最小
高斯平行信道
一个
则:
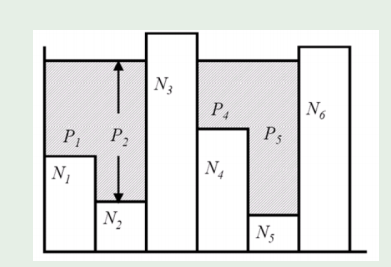
用注水法则,信道总功率是一定的(
(噪声过大的信道传输效率为0)
可结合信道总功率等于各个信道功率之和求出
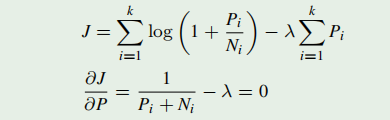
带限(模拟)高斯信道的容量
qtmd
模拟高斯信道的容量
qtmd
传输1bit所需的最小能量
qtmd