引言:
常微分方程(Ordinary Differential Equations,ODEs)模型是描述自然、工程和社会科学中许多动态系统行为的数学模型。常微分方程模型包含一个或多个未知函数及其导数,用于描述系统中的变化和相互作用。本文将介绍如何使用常微分方程去解决追逐问题和最速降线问题。
1 追逐问题
- 一商船与一海盗船从不同的地点同时出发,两船可实时观测到对方的位置。
- 两船均沿直线航行,海盗船在确定航行方向前可观测到商船的航行方向。
- 两船在航行过程中保持速度不变,海盗船的速度是商船的
倍 我们需要解决的问题时,商船能否逃离海盗船的追逐
建立数学模型,以海盗船初始位置为原点,商船初始位置为
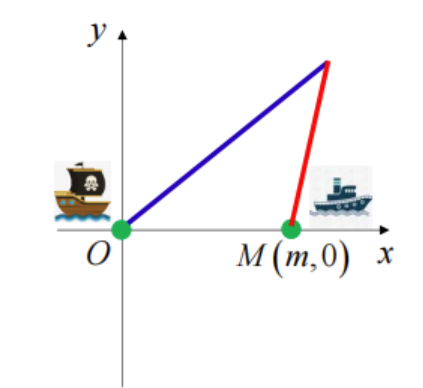
若在某一时刻,海盗船与商船位于同一地点
,那么根据速度与路程的公式可以得到 ,即: 根据上式可以得出 的轨迹为圆 那么设A轨迹的圆心为 ,半径为 的圆C 下面我们尝试在直角坐标系中表示这个圆,因为圆心的位置是不确定的,这取决于 的大小。 根据 的正负,对其进行分类讨论 若
,那么 , - 点O在圆C外,M在圆C内,在这种情况下, 不论商船以何方向航行,海盗船均能在一定时间后与商船相遇。
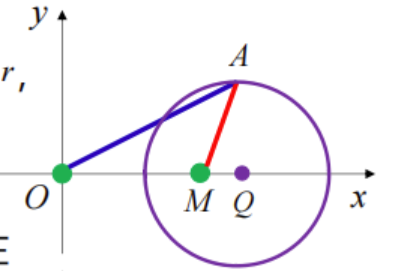
- 点O在圆C外,M在圆C内,在这种情况下, 不论商船以何方向航行,海盗船均能在一定时间后与商船相遇。
若
, - 此时M在圆C外,O在圆C内。
- 这时我们令
,当商船航向与商船和海盗船连线的夹角不超过 时,海盗船均能在一定时间后与商船相遇 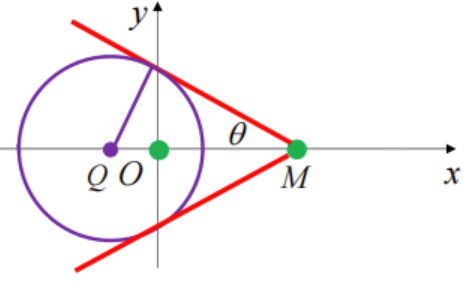
下面升级一下条件:
- 一商船与一海盗船从不同地点同时出发,两船可实时观测到对方的位置
- 商船沿直线航行,航向垂直于链接商船于海盗船初始位置的直线。在任意时刻,海盗船的航行方向为链接商船与海盗船此时位置的直线的方向。
- 商船和海盗船的速率分别为
和 , ,两船在航行过程中保持速率不变。 - 求海盗船在与商船相遇前的航行轨迹
同样的,以海盗船的起始位置为原点,商船的初始位置为
这里我们引入时间维度,即时刻
根据上述切线方程,我们也可以得到一个关于t的式子,将两式联立:
对两边同时积分:
2 最速降线问题
- 最速降线
- 给定垂直平面上的两点
,一质点以何路径从 运动到 ,可使运动时间最短
- 给定垂直平面上的两点
2.1 直线下降
- 给定垂直平面上两点
,一质点沿连接 的直线轨道从 运动到 ,求质点的运动时间
我们设
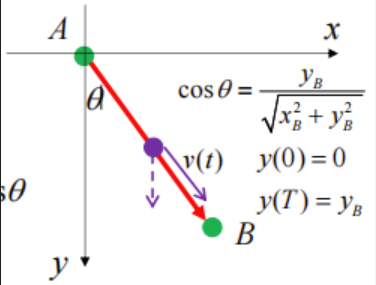
- 质点下降的过程中势能全部转化为动能,有
由题意可知 根据物理学知识易得: 当 时,有:
2.2 圆弧下降
- 一质点沿圆心为
,半径为 的圆弧轨道从 运动到 ,求该质点的运动时间 设质点开始运动时刻为 , 时刻质点所在位置x轴夹角为 ,速率为 可以得到, 时刻,质点的纵坐标为 ,质点运动过的距离为
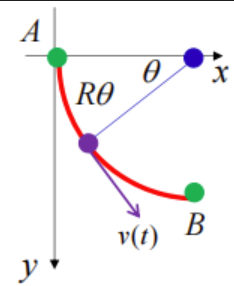
由能量守恒定律得:
2.3 光的折射与最速降线
在介绍最速降线的问题之前,先研究一下光的折射问题。
光的折射
- 折射率:标志介质的光学性质的量,折射率为
的介质中的光速为 ,其中 为真空中光的传播速度
- 折射率:标志介质的光学性质的量,折射率为
定律: ,C为常数 原理 - 光沿着所需时间最短的路径从一点传播到另一点
定律 - 设光在点
所在介质中的传播速度分别为 , 与两介质交界面的垂直距离分别为 , 间的水平距离为
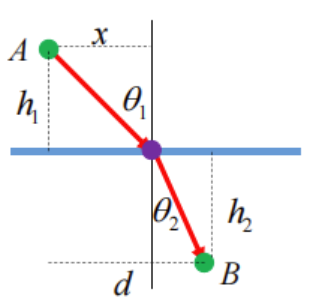
现在设光经过交界面上与
水平距离为 的点,光传播所需时间为: 对x求导得:(因为匀速运动,所以导数为0) 根据各种数值关系化简得: - 设光在点
最速降线
将平行于
现在设质点经过
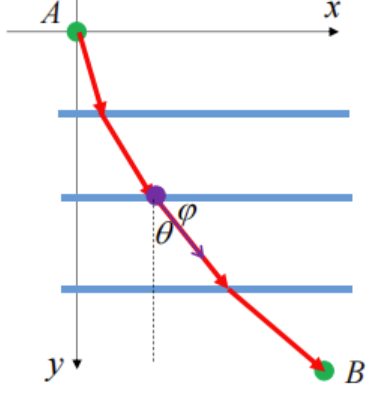
整理上式,得到: