差分方程模型

引言:

差分方程是描述离散时间系统动态特性的数学方程。与常微分方程不同，差分方程是在离散时间步上描述系统行为的。它在许多领域中被广泛应用。本文主要介绍差分方程的一些特性，并利用差分方程去解决一些实际问题——蛛网模型与种群增长模型。

差分方程

差分
- 设是依赖于整数变量的函数， $称为的差分$
差分方程（Difference equation）
- 含有未知函数的有限差分的方程
阶线性差分方程
- - 齐次的:
  - 常系数: 同理可得：
二阶线性常系数其次差分方程
- 二阶线性常系数齐次差分方程的一般形式为
- 若存在是差分方程的解，那么也是差分方程的解；若和都是差分方程的解，则也是差分方程的解
- 若是差分方程的解，则一定满足

因为方程是其次的，所以对于而言，无论只要存在是他的解，不论前面的系数是什么，最后都会被消掉。

特征方程：
- 若特征方程会有两个不同的根
  - 差分方程的通解为,其中是常数
  - 如果，当且仅当
- 若特征方程只有一个根，那么, 根
  - 差分方程的通解为,其中为常数
  - 当且仅当

微观经济学模型

这里我们定义商品的价格为
需求:
- 一种商品的需求是消费者在一定室内在各种可能的价格水平下，愿意并且能够购买该商品的数量
- 需求函数表示一种商品的需求熟练和影响该需求数量的各种因素之间的相互关系
  - 需求函数（减函数反函数）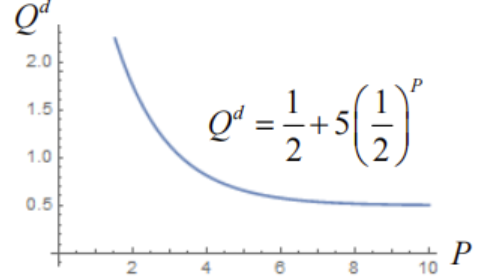
供给
- 一种商品的供给是指生产者在一定时期内在各种可能的价格水平下，愿意并且能给提供出售的该商品的数量
- 供给函数表示一种商品的供给量与影响该商品的供给量的各种因素之间的相互关系
  - 供给函数（增函数）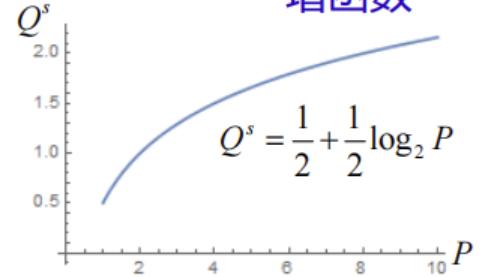
均衡：
- 均衡指一种平衡状态，即相对静止状态，如果没有其他因素扰动，这个状态会一直持续下去
- 均衡价格
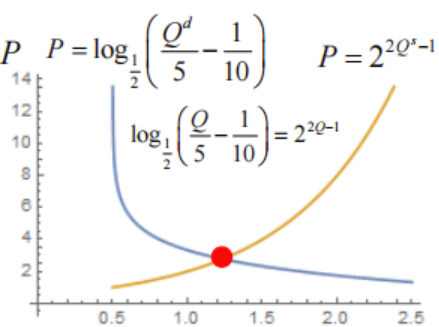
  - 市场上某种商品的需求量和供给量相等时的价格。均衡价格水平下的相等的供求数量称之为均衡数量

在微观经济学的分析中，为了简化分析过程我们大多采用线性的需求函数和供给函数。同时在动态均衡价格模型中，对于生产周期比较长的商品，商品的供给量通常是由前一生产周期的价格决定的，即：

蛛网模型

蛛网模型是研究某些生产周期较长且不宜储存的商品均衡价格的动态稳定性的模型

记在周期某种商品的供求量为价格为需求函数,需求函数的反函数,供给函数，均衡点满足和（即同时满足需求函数和供给函数）

这里我们说的需求函数和供给函数均为线性函数即其中为商品需求量减少一个单位时的价格上涨两，为商品价格上涨一个单位时需求量的减少量为商品价格上涨一个单位时（下一周期）供给量的增加量 - 有如下递推关系 - 即 - 数列收敛的充要条件是

同样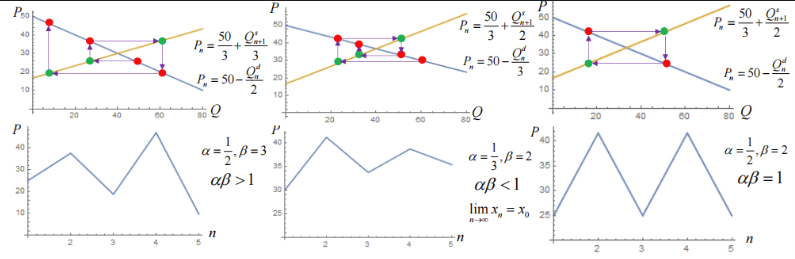的值也决定了这个体系是否是稳定均衡 - 若则为稳定均衡，否则是不稳定均衡。这和数列的收敛性有很大关系

下面我们假设商品的供求量由前两个周期的价格决定 - 即需求函数,需求函数的反函数，供给函数 - 此时供给函数可以简化为前面我们说到，均衡点满足和由此可以得出：即：

整理得：令此时当且仅当

现在回到差分方程的问题，需要得到在什么情况下，所得到的价格体系是稳定均衡的。 已知蛛网模型的差分方程为，我们设它的特征值为，那么它的特征方程为：

利用求根公式解得：

为了让是收敛的，那么就必须让：

根据上述方程，我们必须保证，即但是这种情况下，,这是不符合要求的。所以在这里我们引入虚数去放宽条件，不必保证是实根。

讨论的情况，此时: 计算一个虚数的模：此时我们保证: 求出: 此时价格体系是稳定均衡的。

种群增长模型

离散单种种群模型
- 现实种群由一个世代构成，相继世代之间没有重叠
- 记为第代个体数量，数列满足差分方程
指数增长模型
- 每一代个体繁殖的个体数量与该代个体数量之比是一个常数即
- 很容易得出，如果则单调递减趋近于0，若,x_n单调递增趋于

Logistic模型

种群增长率仅与种群数量有关且是种群数量的递减函数
, 增长量，增长率
内禀增长率 ,环境承载量

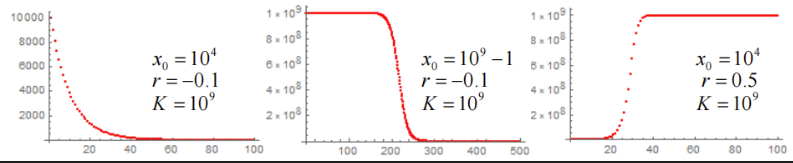
平衡点
- 若差分方程满足的点为平衡点
- 若，则
- 只要初始点与平衡点充分接近，即,则称之为渐近稳定

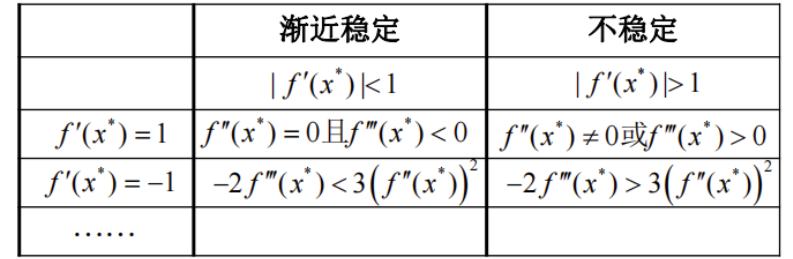
周期点
- 差分方程满足的点称为周期点，这里的通过以下方式定义
- 根据上述平衡点的性质，易得: 的k周期点就是差分方程的平衡点，且前者的渐近稳定性后者决定。

> 也就是对某个初始点进行k次迭代，所得到的结果，如果经过K次迭代所得的结果与一致，那么此时的x称为周期点。 > 把这个问题放到微积分中看，他与函数在某一点的收敛性有关。

logistic模型的2-周期点

2-周期点即: 现在已知：计算

两者相等，计算设方程存在四根，,讨论剩下两根：将两根交叉带入计算的导数：

为了让函数收敛，即让模型在该点处渐近稳定，我们需要让即：