群试问题——伪币辨识

引言:

12枚外观相同的硬币中有一枚是伪币，伪币质量与真币不同，天平一次测量只能比较两端质量的大小，不能读出质量数值，能否用天平测量三次找出伪币，并说明伪币相对真币偏轻或偏重？伪币辨识问题是著名的群试问题，本文将介绍如何利用Dyson集来解决伪币辨识问题，以及如何在枚伪币只能测量次的情况下，巧妙地构造Dyson集。

伪币辨识

  • 12枚外观相同的硬币中有一枚是伪币，伪币质量与真币不同
  • 天平一次测量只能比较两端质量的大小，不能读出质量数值
  • 能否用天平测量三次找出伪币，并说明伪币相对真币偏轻或偏重

分析：

  • 硬币真伪的可能性有种，每一种测量结果对应一种可能性，不同测量结果对应的可能性各不相同 自适应与非自适应：
  • 后一次测量依赖于之前的称量结果的方案称为自适应的，否则称为非自适应的。

单伪币最优方案：

  • 对任意整数
    • 若,则存在一非适应的测量方案，用w次称量即可从枚硬币中辨别伪币并确定轻重。
    • 若,则不存在自适应的测量方案，用次测量即可从枚硬币中辨别伪币，并确定轻重。
Dyson集
  • 满足以下条件的元向量子集称为Dyson集
    • 满足
    • 满足 若,则
  • 若存在含个元向量的Dyson集，则可用非自适应方案经w次测量从n枚硬币中辨别伪币并确定轻重。

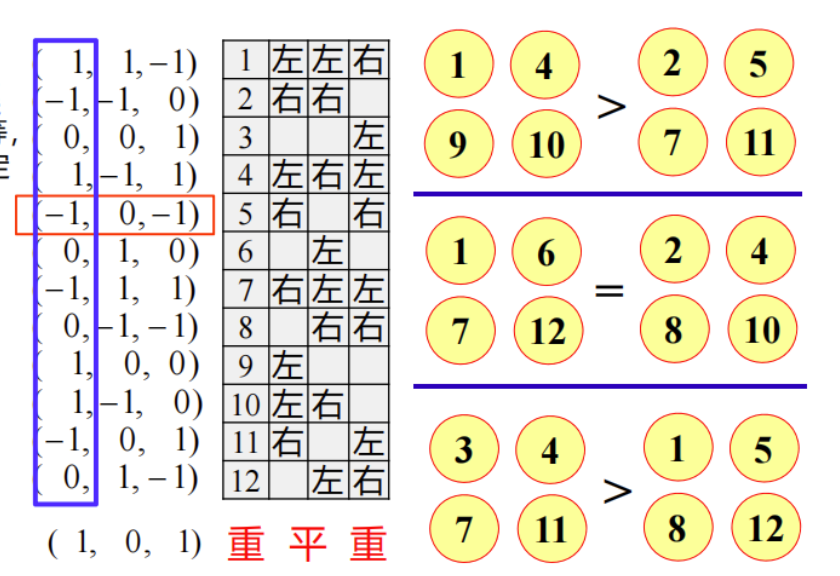
可以看到，在三次测量中硬币1分别在左，左，右，所以他对应的向量子为。我们用这种方式去定义所有的向量子，总共右12个向量子。

现在根据天平判断结果推测 - 第一轮天平左重右轻，则伪币一定参与了测量

  • 第二轮天平是平的，则伪币一定没有参与测量

  • 第三轮伪币左重右轻，则伪币一定参与了测量且与第一轮处在同一边。 所以，伪币所对应的向量子为或 进行查找，即可从个向量子中找到对应伪币的编号了。

  • Dyson集的构造

    • 令
    • 令
    • 记
      • 中向量两两不同
      • 对任意
    • 记
      • ，与在中至多出现一次 对于Dyson集的构造我们提出了如下的要求：

  • 如何在与恰取一个的情况下保证

  • 如何保证与在不同的子集中不被重复选取

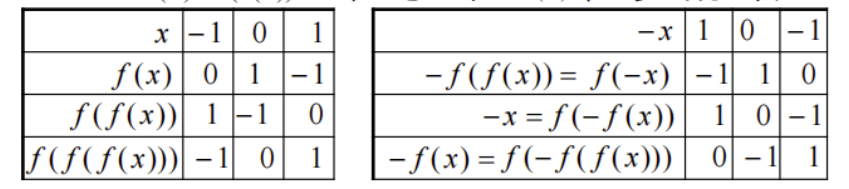
  • 寻找中个向量，使得

  • 不同n值时的Dyson集

    • 满足
    • 满足 举例：当时，我们构造相应的Dyson集：